EL ESTUDIO DE LOS GIRASOLES: EL EXPERIMENTO INACABADO DE TURING

Uno de los últimos estudios de Turing antes de su suicidio fue el que realizó sobre la morfogénesis en las plantas.

En el Festival de la Ciencia de Manchester del año 2012, como parte de las celebraciones del Centenario de su nacimiento, se invitó a los ciudadanos de esta ciudad a que hicieran uno de los experimentos que Turing dejó sin concluir. Su fascinación por las secuencias de números y los patrones con formas geométricas le llevó a pensar que el número de pétalos de las plantas o la disposición de las semillas de los girasoles se ajustan a la sucesión de  Fibonacci. Al parecer Turing se inspiró en el trabajo publicado en 1938 por J.C. Schoute, quien estudió esta cuestión en 319 girasoles. Lamentablemente, este y otros proyectos fueron abandonados en 1952 tras su detención y condena por haber mantenido relaciones homosexuales.

Describiremos a continuación el protocolo del experimento con el fin de que pueda ser reproducido de manera sencilla. En primer lugar, se siembran de una a cinco semillas de girasol por maceta, que estarán colocadas en un lugar soleado, de manera que estén a una temperatura de entre 13 ºC y 30 ºC, y tengan luz abundante. Las semillas se regarán sin llegar al exceso de agua. Sobre la especie a plantar, se recomienda consultar en una floristería la que mejor se adapte a estar en una maceta, dado que hay varias especies -por ejemplo, el girasol rojo, una especie más “ornamental”, el girasol gigante o Mammoth, o la Rayo de sol, que pintara Van Gogh en sus célebres cuadros-.

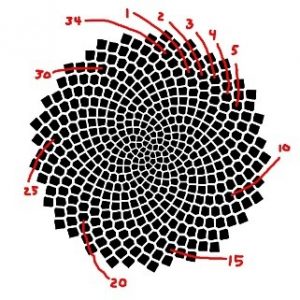
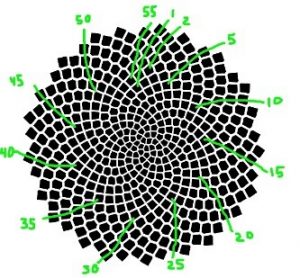
En segundo lugar, cuando llegue el momento,  contaremos las espirales sobre las que se ubican las semillas o pipas en la flor. Pero ¿cómo podemos llevar a cabo una tarea así? Según el Museo de las Matemáticas de Nueva York, si contamos las espirales tal como indica su procedimiento (consultar su página web: http://momath.org/ ), encontraremos que el resultado es siempre un número de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…) y, por tanto, comenzando la secuencia con los valores 0 y 1, los números restantes serán la suma de los dos anteriores (xn= xn-1 + xn-2).

En tercer lugar, y esto es lo más sorprendente, si dividimos un número de Fibonacci por el anterior, por ejemplo 55/34, obtendremos un número que se aproxima a la llamada proporción áurea, cuyo valor es 1,61803. Se trata de un número que representa un canon de belleza utilizado en arquitectura y en arte, y que también se halla en la naturaleza. Este se puede obtener a partir de la siguiente expresión:  φ = (1 + √5)/2